Алгоритм LSA для поиска похожих документов

И снова наш аналитический отдел подготовил материал для читателей блога Netpeak. Передаю привет Кириллу Левенцу — он проделал титанический труд, чтобы изложить понятным языком не самые простые вещи.

Среди огромного числа алгоритмов, которые используются для поиска и анализа информации, особое место занимают те, чья цель — обнаружение скрытых закономерностей или неочевидных зависимостей.

Используя семантический анализ текста, мы можем сказать, например, что два текста похожи, даже если эта похожесть выражена косвенно. Или например «лыжи» и «автомобиль» по отдельности относятся к разным категориям, но будучи использованы вместе, могут быть интерпретированы в таких категориях, как «спорт» и «отдых».

Об одном из методов, который применяется для рекомендательных систем (коллаборативная фильтрация), информационного семантического поиска, разделения текстов по тематикам без обучения и многих других и пойдет речь далее. Метод этот называется латентно-семантическим анализом (LSA — Latent semantic analysis). Можно сказать, что это продвинутый SEO анализ текста.

Рассмотрим более подробно, что это за метод и как он работает

Уже из названия можно сделать вывод о том, что он должен делать, а именно находить скрытые смысловые взаимосвязи между объектами (будь-то слова в тексте или товары в магазине). Для текстов на естественных языках такой скрытой закономерностью может быть, например, наличие определенного набора слов в определенной теме. Представим себе такую задачу: у нас есть коллекция документов и мы хотим научиться отвечать на вопрос: два документа близки по тематике или нет. Вывод о схожести можно сделать, основываясь на том, какие слова и в каких пропорциях входят в каждый из документов.

Чтобы подготовить данные для этой задачи, используют подход, который называется «мешок слов».

Его суть состоит в том, что для нас неважен порядок слов в документе, в каких морфологических формах они представлены, а важно только количество вхождений конкретных слов. Предположим, что каждую тему можно охарактеризовать определенным набором слов и частотой их появления. Если в тексте конкретный набор слов употребляется с определенными частотами, то текст принадлежит к определенной теме.

Основываясь только на этой информации, строится таблица «слово-документ». Где строки соответствуют словам (а точнее, их леммам), а столбцы - документам. В каждой ячейке хранится 1, если слово есть в документе, и 0 - если нет. Хотя такой вариант и самый простой, но не самый лучший. Вместо 0 и 1 можно использовать, например, частоту слова в документе или tf-idf слова. Такой способ представления текстов в виде таблицы (или матрицы) называется векторной моделью текста. Теперь, для того чтобы сравнить два документа, нужно определить меру схожести двух столбцов таблицы.

Сделать это можно по-разному:

• скалярное произведение векторов - столбцов таблицы;
• косинусное расстояние (пожалуй самое адекватное);
• евклидовым расстоянием;
• манхэттенским расстоянием.

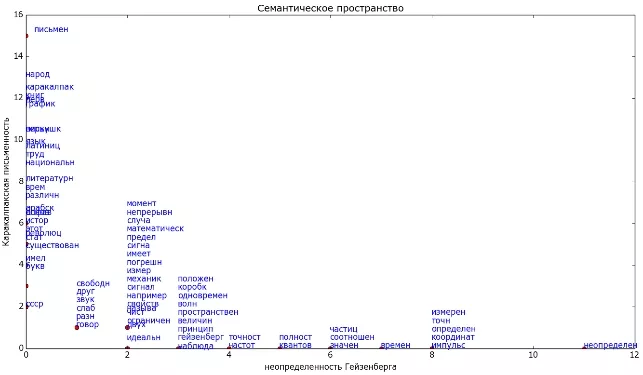
Чтобы лучше понять все вышесказанное, изобразим это графически на простом примере двух небольших текстов. Один  текст про письменность, другой про неопределенность Гейзенберга. Стоп-слова удалены, а остальные приведены к основной форме (без окончаний). Каждая точка на графике — слово. На осях отложено, сколько раз слово встретилось в каждом документе. Т.е. если слово встретилось в тексте про неопределенность 3 раза, а в тексте про письменность 2 раза, то на рисунке это слово изобразим точкой с координатами (3,2).

Видно, что в этом примере некоторые слова встречались и в одном и в другом тексте приблизительно одинаково часто («свободн», «друг», «звук» и так далее). Такие слова не дают возможности отличить тексты один от другого и в принципе сравнимы со стоп-словами. Но есть слова, которые характерны только одному из текстов. Имея такое представление текста, мы можем определять близость каждого слова к теме (как косинус угла между вектором с началом в (0;0) и концом в точке слова и осью, соответствующей документу). Если же такого слова в коллекции нету, то о нем мы ничего не можем сказать.

Для сравнения документов можно подсчитать сумму векторов-слов, которые в них входят и опять же оценить расстояние между ними. В рассмотренном примере слова распределились хорошо, так как тематики существенно разные. А если тематики схожи, то может получиться такая картина: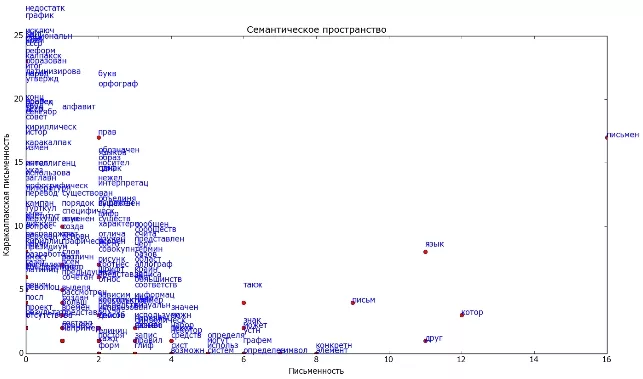

По сравнению с предыдущей картинкой видно, что документы существенно похожи, и, кроме того, есть слова, которые характеризуют общую тематику для обоих текстов (например "язык" и "письмен"). Такие слова можно назвать ключевыми для данной темы. Т.е. напрашивается вывод, что имея такое представление текстов, мы теоретически можем сгруппировать документы по близости их содержимого, и таким образом построить тематическое разбиение коллекции текстов. В частности может оказаться, что каждый документ - это отдельная тема. Также можно искать документы по запросу, при этом могут находиться документы, которые не содержат слов из запроса, но близки ему по теме.

Но в жизни оказывается, что документов и слов очень много (гораздо больше чем тем) и возникают следующие проблемы:

• размерности (вычисление близости между векторами становится медленной процедурой);
• зашумленности (например, посторонние небольшие вставки текста не должны влиять на тематику);
• разряженности (большинство ячеек в таблице будут нулевыми).

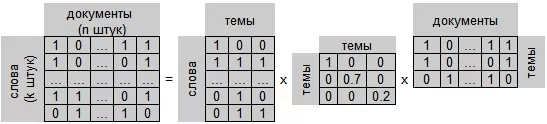
В таких условиях довольно логично выглядит идея, вместо таблицы "слово-документ" использовать что-то типа "слово-тема" и "тема-документ". Решение именно такой задачи предлагает LSA. Правда, интерпретация полученных результатов может оказаться затруднительной.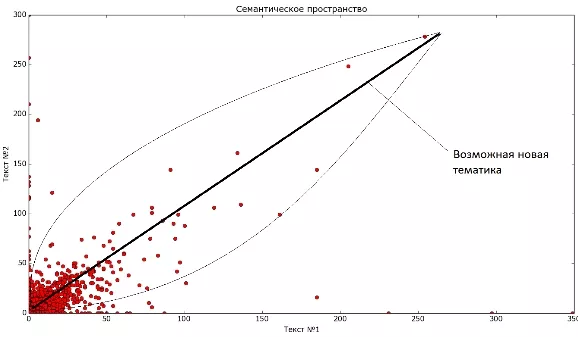

На рисунке приведен пример карты двух художественных текстов. Видно, что у них есть как свои особенности, так и много общего, и можно выделить новую тематику. Если говорить в терминах линейной алгебры, то нам нужно такое представление:

Числа в таблицах в общем случае не обязательно будут именно 0 и 1. Имея такое представление, мы можем кроме оценки близости слов и документов, также определять важные слова для каждой тематики.

Ограничения LSA:

1. Невозможно получить тематик больше чем документов/слов.
2. Семантическое значение документа определяется набором слов, которые, как правило, идут вместе.
3. Документы рассматриваются как просто наборы слов. Порядок слов в доку­ментах игнорируется. Важно только то, сколько раз то или иное слово встречается в документе.
4. Каждое слово имеет единственное значение.
5. Недостаток LSA — предположение о том, что карта слов в документах не имеет вид нормального распределения. С этой проблемой справляются другие модификации метода (вероятностный LSA и LDA).

LSA включает в себя следующие этапы:

1. Удаление стоп-слов, стемминг или лемматизация слов в документах;
2. Исключение слов, встречающихся в единственном экземпляре;
3. Построение матрицы слово-документ (бинарную есть/нет слова, число вхождений или tf-idf);
4. Разложение матрицы методом SVD (A = U * V * WT);
5. Выделение строк матрицы U и столбцов W, которые соответствуют наибольшим сингуляр­ным числам (их может быть от 2-х до минимума из числа терминов и документов). Конкретное количество учитываемых собственных чисел определяется предполагаемым количеством семантических тем в задаче. А вообще чем больше сингулярное число, тем сильнее в коллекции проявлена тема.

В итоге получается нечто такое:

Пример с небольшими документами

[Взят из статьи Indexing by Latent Semantic Analysis, Scott Deerwester, Susan T. Dumais, George W. Furnas, and Thomas K. Landauer, Richard Harshman]

Пусть имеется следующий набор заголовков-документов:

• c1: Human machine interface for ABC computer applications
• c2: A survey of user opinion of computer system response time
• c3: The EPS user interface management system
• c4: System and human system engineering testing of EPS
• c5: Relation of user perceived response time to error measurement
• m1: The generation of random, binary, ordered trees
• m2: The intersection graph of paths in trees
• m3: Graph minors IV: Widths of trees and well-quasi-ordering
• m4: Graph minors: A survey

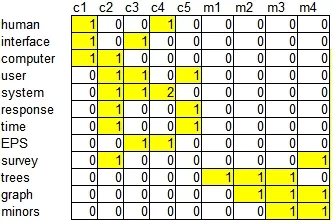
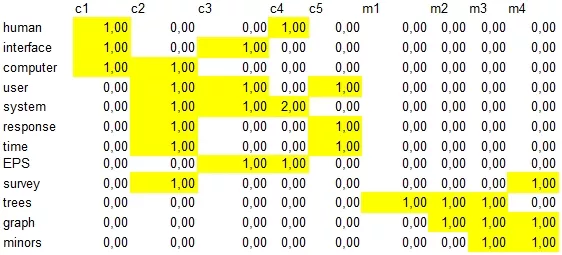
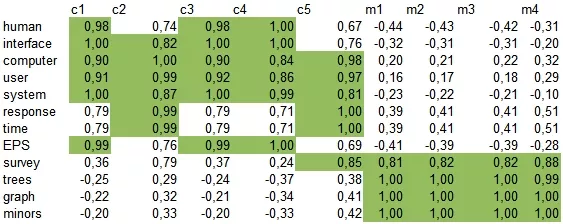
Выделяем слова, которые встретились хотя бы в двух заголовках. И строим матрицу слово-документ: в ячейках будем писать количество вхождений слова в до­кумент.

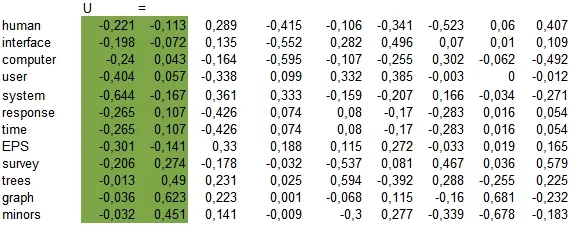
Применяем сингулярное разложение к этой матрице и получаем три матрицы (U, V, W^T).

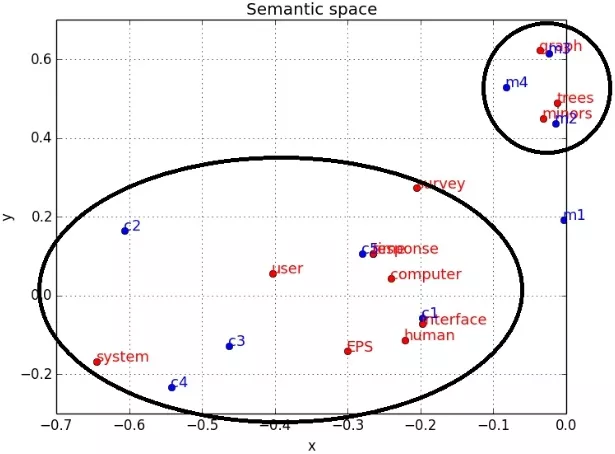
Чтобы иметь возможность визуально оценить результат, выделим только две главные компоненты, соответствующие самым большим сингулярным числам. Используем значения в выделенных столб­цах как координаты и изобразим их в виде точек на плоскости (синим цветом документы, красным - слова, кругами - возможные тематики).

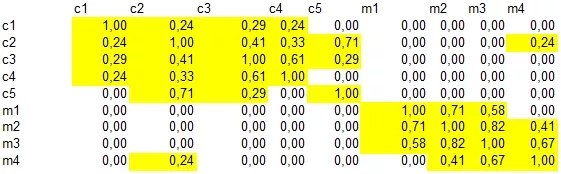
Рассмотрим расстояние между каждой парой слов. Было (желтым цветом выделены значения выше 0):

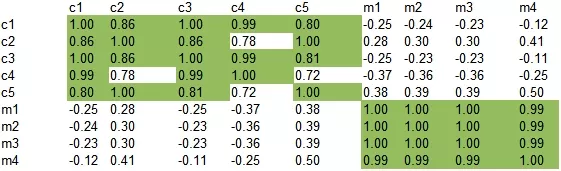
Стало после снижения размерности (зеленым цветом выделены значения больше 0,8):

Как и по картинке, так и по таблице видно, что термины образовали 2 группы (довольно условно) и по сравнению с исходной матрицей связи значительно усилены (как укрепились исходные, так и появились новые):

• [human, interface, computer, user, EPS, response, time],
• [survey, trees, graph, minors].

Между каждой парой документов.

Было:

Стало:

Отношение термин документ.

Было:

Стало:

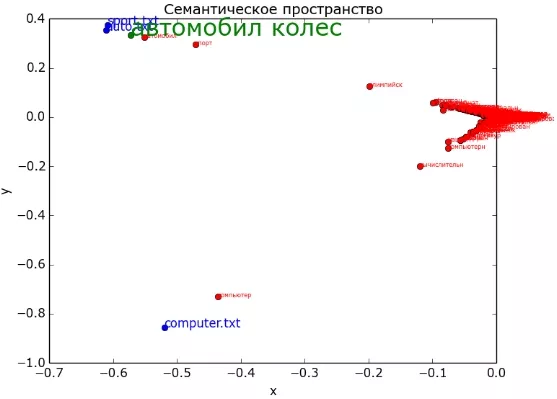
Рассмотрим еще один пример: пусть имеются три документа, каждый - на свою тематику (первый про автомобили, второй про спорт и третий про компьютеры). Используя LSA, изобразим двумерное представление семантического пространства, и как в нем будут представлены слова (красным цветом), запросы (зеленым) и документы (синим). Напомню, что все слова в документах и запросах прошли процедуру лемматизации или стемминга.

Видно, что тема "компьютер" хорошо отделилась от двух других. А вот "спорт" и "авто" довольно близки друг другу. Для каждой темы проявились свои ключевые слова. Зеленым на рисунке изображен запрос "автомобил колес". Его релевантность к документам имеет следующий вид:

1. 'sport.txt' - 0.99990845
2. 'auto.txt' - 0.99987185
3. 'computer.txt' - 0.031289458

Из-за близости тем "спорт" и "авто" довольно сложно точно определить, к какой теме он принадлежит. Но точно не к "компьютерам". Если в системе, обученной на этих документах, попытаться определить релевантность к образовавшимся темам слова "рынок", то в ответ мы получим 0 (т.к. это слово в документах не встречалось ни разу). Добавим в систему документ по теме "финансы". Будем снова искать слово "рынок".

Получим следующую картинку:

Релевантность к темам будет такой:

1. 'finance.txt' - 0.99948204
2. 'sport.txt' - 0.97155833
3. 'auto.txt' - 0.23889101
4. 'computer.txt' - -0.24506855

Итак подведем итог:

1. LSA позволяет снизить размерность данных - не нужно хранить всю матрицу слово-документ, достаточно только сравнительно небольшого набора числовых значений для описания каждого слова и документа.
2. Получаем семантическое представление слов и документов - это позволяет находить неочевидные связи между словами и документами.
3. Из минусов - очень большая вычислительная сложность метода.